まず部分分数変数の方程式を立て、それを使って連立方程式を立てます。 タップしてもっと手順を表示する 方程式の各辺の係数 が等しくなるようにして、部分分数変数の方程式を立てます。係数が分数になっているときは, 分母の最小公倍数 を両辺に掛けて,分母を払って整数係数に直してから解きます.(最小公倍数が分からないときは, 分母の数字を全部掛けて もかまわない) なお, のように,文字が分子に書いてあるものと横に書いてあるものは,同じものです は と同じ (答案) (1)の両辺を12倍して整数係数に直す (1') (2)の両辺を6倍して整数係数に直す (2') (1')×2− と連立方程式に苦戦している方のために、「 連立方程式の解の3パターン(解あり、任意の解、解なし) 」をそれぞれ分かりやすく解説します! ついでに同次形の連立方程式の解法も最後に説明しているので良かったらご覧ください。

中2数学 いろいろな連立方程式の解き方 学習プリント 練習問題 無料ダウンロード印刷
連立方程式 解き方 分数と小数
連立方程式 解き方 分数と小数-次の連立方程式を解きなさい 8 3 x 1 2 y= 11 6 の両辺に6をかけて分母をはらって式を整理すると16x3y=11 辺々引くと 7x3y = 7 ) 16x3y = 11 9x = 18 両辺を9で割るとx=2 x=2を7x3y=7に代入すると 143y=7 3y=21 y=7 2xy= 29 3 の両辺に3をかけて分母をはらって式を整理すると6x3y=29 1 6 x 3 4 y= 13 12 の両辺に12をかけて分母をはらって式を整理すると2x9y=13 2x9y=13 連立方程式の解の求め方、分数がある場合 9 連立方程式の解の求め方、小数がある場合 10 連立方程式の解の求め方、A=B=Cの場合 11 連立方程式の解の求め方、比の場合 12 動画で理解しよう! ここまでの内容だよ 連立方程式 2x 3y = 1 2 x 3 y = 1 のように、 2 2 つの文字を含む一次方程式のことを二元一次方程式といいます。 2 2 つ以上の方程式を組み合わせたものを 連立方程式




中2数学 連立方程式 応用 2つの連立方程式が同じ解をもつときのa Bの値を求める 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト
「方程式」→「連立一次方程式を解く」 →「方程式の数」として3を入力→OK 方程式1: 2*x3*y4*z=5 方程式2: xy3*z=6 方程式3: 3*x4*y5*z=7 変数: x,y,z と入力してOKボタンをクリック 結果⇒ ※wxMaximaでは分数の解も既約分数で表示されます.Y=4 (答) x=3, y=4 この問題のように一方の式を少し変形すれば y について解かれた形 になるときは、この式を使って y が消去できます。 → (3) (3)の結果を (1)に代入すると y も求まります。 ※加減法でもできますが、ここでは代入法で行った場合の答案を小数・分数は、何倍かして整数にしてから加減する → 係数を整数にした式を作ってから方程式を解きなさい。 (3) = − = 04 24 4 30 5 x y x y (4) − = − = 5 2 1 3 2 y x x y 連立方程式④ 連立方程式の解き方(2)B 学 年 年 年 組 氏名 学習日: 月 日
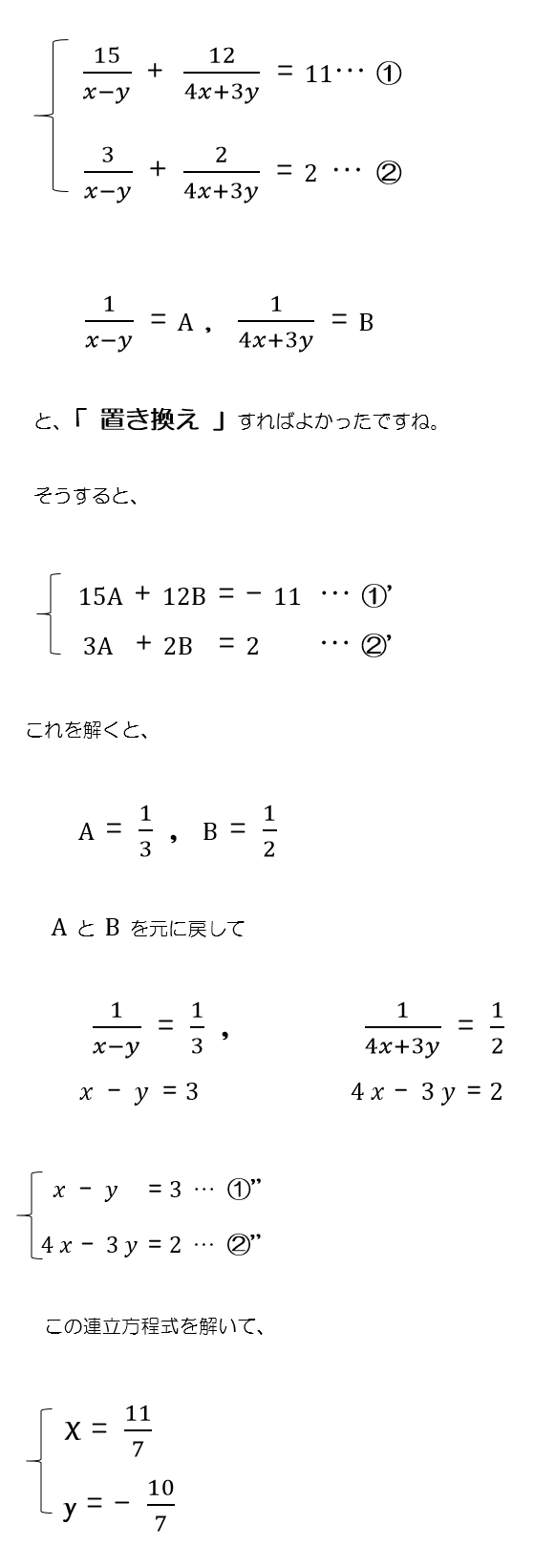
ミカエリスメンテン式の連立方程式のやり方誰かわかりますか?この例題の解き方がわかりません。 お 私の解き方↓ 6km→6000m 分→分(そのまま) 6000×=1000 1000→1km 単位を揃えて解いたはずです。 これもまた連立方程式のつまずきポイントの代表格ではないでしょうか。 対策法はいくつかありますが、オススメは2つです。 1つは「 図を書くこと 」、もう1つは「 わからないものを箇条書きにすること 」です。 まず、図を書くことは全体の状況を理解この、分数の文字を別の文字で置き換える解き方は、 分母に文字がある連立方程式ではよく使う よ ただし! 1 x − 1 y = − 5 2 1 x − 1 y = − 5 2 ― , 8 x−2 2 y1 = 10 8 x − 2 2 y 1 = 10 ― であるとき、 x,y x, y の値を求めよ。 みたいに、 と で 分母が異なってて、 置き換えても楽にならない場合がある から気を付けてね はかせちゃん こういうときの置き換えの文字ってなぜか大文字ですよね 機関の
次の連立方程式を解け。 (1) 文字を消去すべし! ⇒ と変形して、代入法を用いて解いていきましょう。 (2)の解き方、考え方 問題 次の連立方程式を解け。 (2) こちらも (1)と同じように、文字を消去することを考えましょう。 一次式である を変形して、 に代入して解いていきます。 (3)の解き方、考え方 問題 次の連立方程式を解け。 (3) (1)(2)とは違い、文字を消 やりました かずのかず 連立方程式の計算は こちらで 確認してくださいね 中2数学「連立方程式の計算」の問題 どこよりも簡単な解き方・求め方 今回は、2つの方程式を組みにした「連立方程式」を学習します 中2数学で一番大切と言っても良い単元中学1年の数学で習う方程式は一次方程式と呼ばれます。 2年、3年に習う連立方程式や2次方程式の基礎となっています。 ここでは カッコのある方程式 、 分数、小数が含まれる方程式の解き方 や ケアレスミスをしがちなところ などを説明しています。 基本となるところですので、しっかり



Tossランド いろいろな連立方程式




世界一わかりやすい数学問題集中2 2章 連立方程式
普通、連立方程式はこのように解きます。しかし連立方程式は、行列によっても解くことが可能です。次に、それについて見ていきましょう。 12 行列を使った解き方 まず、上の連立方程式は、行列を使うと次のように表現することができます。 \係数に分数のある連立方程式 係数に分数がある場合、両辺に分母の公倍数をかけて係数を整数にすると計算しやすくなる 必ずしも最小公倍数にこだわらなくてもよい 例 { 1 2 x 1 3 y = 2 ・・・① 2 5 x 2 3 y = 2 5 ・・・② ①の両辺に6をかけて、②の両辺に15をかけて係数を整数にする { 3x2y = 12 ・・・①' 6x10y = 6 ・・・②' ①'×2②' 6x4y = 24 ) 6x10y = 6 6y = 18 y = 3この形の方程式を解くとき,普通の方程式を解くときの 「移項」のような変形をしにくい ので,解き方のコツを覚えておくとよいでしょう. 〇「 A=B=C 」というのは,「 A=B かつ B=C 」を省略的に書いたものです.だから,「 A=B=C 」という方程式が与えられ
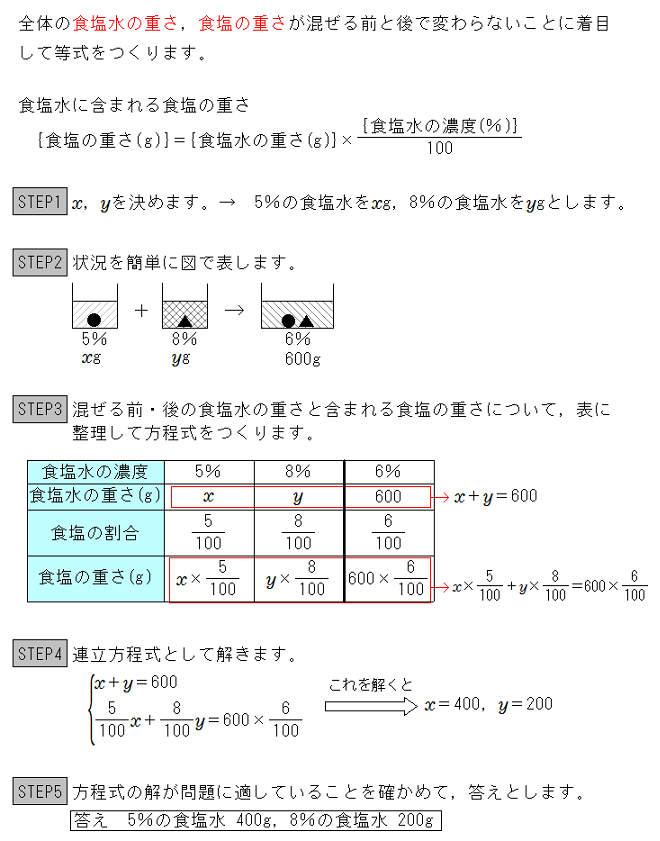



連立方程式 食塩水の問題で連立方程式をつくるコツ 中学数学 定期テスト対策サイト




中2連立方程式の解き方と計算問題 代入法と加減法 Irohabook
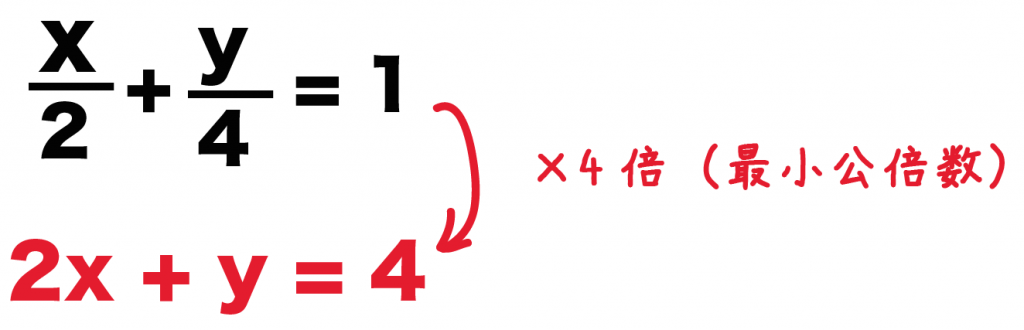
分数がある連立方程式の解き方 小数がある連立方程式と同じように, このままだと計算が大変なので, 掛け算をすることで係数を整数にしていきます。分数を整数にするには, 2つの分母の最小公倍数を考えればよいです。 もし最小公倍数がすぐにわから 分数を含む連立方程式 続いて分数のある連立方程式。 これも難しくない。 ポイントは同じ、「両辺を何倍かする」ことだ。 解き方 \begin{eqnarray} \left\{ \begin{array}{l} \frac{3}{4}x\frac{1}{2}y=3 \\ \frac{1}{2}x\frac{1}{6}y=5 \end{array} \right\end{eqnarray}2 式に分数や小数が含まれる連立方程式の解き方 21 例\begin{eqnarray}\left\{\begin{array}{l}\frac{1}{4}x\frac{1}{6}y=\frac{1}{3}\\05x02y=12\end{array}\right\end{eqnarray} 3 式にかっこが含まれる連立方程式の解き方




連立方程式の解き方 係数に分数がふくまれる場合 Youtube




中学2年数学 連立方程式 加減法を使った連立方程式の解き方 実際に問題を解きながら解説 数学の面白いこと 役に立つことをまとめたサイト
分数を含む連立方程式の加減法の例 分数を含む連立方程式の加減法の例です。この場合、分数が含まれますが、そろえると分数じゃなくなります。 例題 つぎの連立方程式を解いてみます。 解法 (1)消したい文字の係数をそろえる ①の両辺2倍、②の両辺6連立方程式 中学数学2元1次方程式と連立方程式 中学数学連立方程式・加減法 中学数学連立方程式・代入法 中学数学連立方程式 小数・分数;連立方程式の解の比が既知のとき、方程式の1つの係数を算定できます。 例えば「ax2y=1、3xy=5」の解の比が「xy=12」のとき係数aの値を求めます。 解の比は「xy=12 ⇒ 2x=y」のように変形できます。 3つの未知数a、x、yに対して3つの方程式があるので、解が算定できます。 今回は、連立方程式と解の比の関係、意味、例題の求め方について説明します。 連立方程式




中2数学 連立方程式の解き方と定期テスト予想問題 Pikuu



Updated 中学数学 連立方程式 計算問題 For Pc Mac Windows 11 10 8 7 Android Mod Download 22
連立方程式の中に分数の項が混じってる場合の解き方。 漫画で紹介したように、連立方程式の中に分数の項が混じっている問題はどう解いたらよいでしょうか? 簡単です。 一次方程式のときと同じく、 「分母、邪魔!」 と考えて、分母が消えるような数を というわけで、連立方程式においても式の中に分数がある場合には消す! これが鉄則です。 では、それぞれの例題の解き方について順に解説していきます。 分数を含む方程式の解き方を解説! 例題①の解き方、答え1つの方程式の両辺を何倍かしただけでは係数がそろわないときは、それぞれ何倍かしてそろうようにします。 これは分数の通分と同じ考え方です。 この問題では (1)を4倍する と −12y ができ、 (2)を3倍する と 12y ができるので、足し算により y が消去でき




中2数学 3つの文字を含む連立方程式 学習プリント 練習問題 無料ダウンロード印刷




分数をふくむ連立方程式 Youtube
連立方程式の式のつくり方、具体的に解説 (1)数と量の例題 手順1.問題文を分ける。 手順2.条件をすべて書きだす。 例題 かっこ,分数,小数を含む連立方程式1 次の連立方程式を解きなさい。(1) \(\begin{cases}2x\left( 3y\right) =4&\cdots ①\\ 3\left分数の連立方程式の解き方\(1\) 分数の連立方程式を解くときは\(1\)番目に、公倍数を掛けて、分母をはらいます。 分母をはらうときは、分母の公倍数を両辺に掛けます。 問題\(1\) 次の連立方程式を解き



3
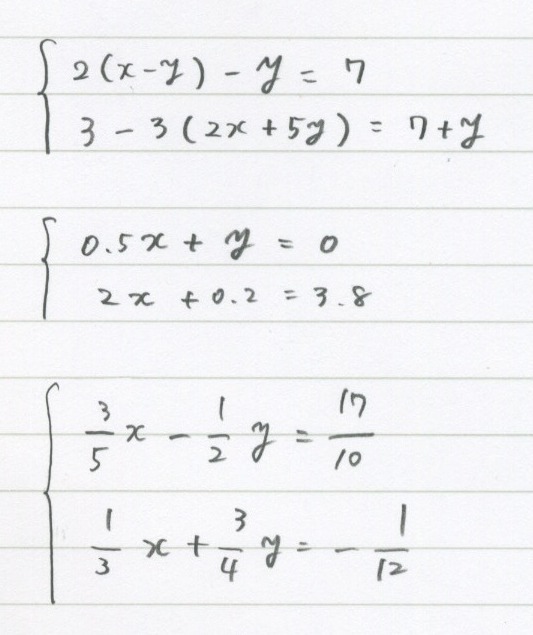



5 2 連立方程式 かっこや分数小数はもうできる 勉強できようサイト
2つの未知数 x, y のどちらかの 係数が等しいとき は、左辺どうし、右辺どうしをそれぞれ 引く と1文字を消去できます。 この問題では y の係数がそろっているので、 y が消去できて x だけの方程式になります。 →(3) (3)の結果を(1)か(2)のどちらかに代入すると、もう一つの未知数も求まります。 例えばこういう問題があったとしよう。これを代入法で解きなさい。 与えられた2つの式の内、1つの式を以下のように変形する。 or (※このケースでは(b)の式を変形した方が楽だよ!) この式を、もう一方の与えられた式(a)に代入する。 xが解ける。 解き方の手順は、化学反応式を作る→係数は未定係数法で求める→単位をmolに換算→係数を比較することで求めたい量を算出する、です。 先ほどの、メタンの燃焼の例で見てみましょう。 ここで、ぜひ覚えて頂きたいのは、 化学反応式の係数は反応に



中学の数学 分数の連立方程式の解き方について質問です の両辺に15 Yahoo 知恵袋




中2数学 カッコ 分数を含む連立方程式 練習編 映像授業のtry It トライイット




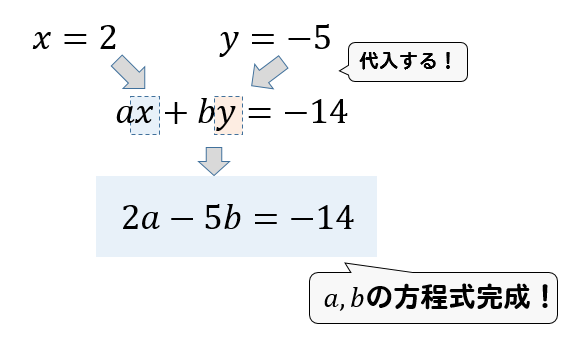
連立方程式の解 xとyに代入して 式が成り立てばok 中学や高校の数学の計算問題



Studydoctor連立方程式の解き方 加減法 中2数学 Studydoctor



連立方程式の文章題 パーセント チーム エン




いろいろな連立方程式 かっこを含む 分数 小数を含む A B C 教遊者



方程式の高校入試問題 連立方程式 方程式の解き方まとめサイト



連立方程式の問題です 答え合わせをしたいので回答お願い致します 3 Yahoo 知恵袋



方程式練習問題 連立方程式の文章問題 割合 パーセント 方程式の解き方まとめサイト




中学2年生 数学 いろいろな連立方程式 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




連立方程式の代入法 簡単な問題で やり方をわかりやすく紹介 中学や高校の数学の計算問題



中学2年生 数学 連立方程式の解き方 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中学2年の数学 動画 連立方程式 加減法の応用編の問題 19ch
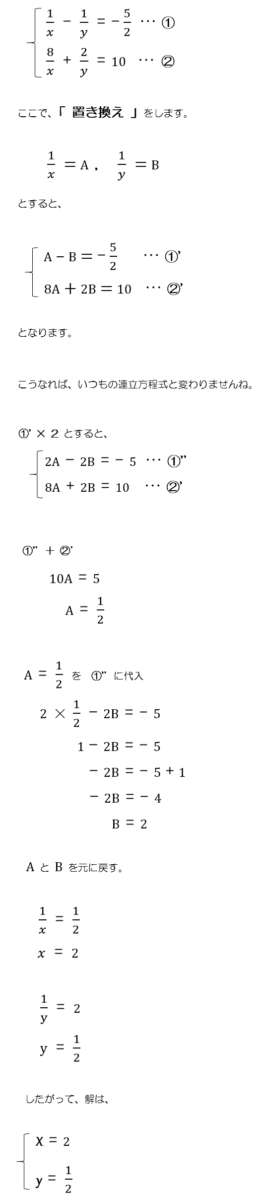



なるほど数学コラム 中学編 8 分母に文字がある連立方程式 を解こう Katekyo学院 教室で個別指導塾ならkatekyo学院 自宅でプロ家庭教師は福島県家庭教師協会 県内各地域で受講可能 福島 郡山 白河 会津 喜多方 いわき 相馬




中2数学 連立方程式 応用 2つの連立方程式が同じ解をもつときのa Bの値を求める 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト




連立方程式の解き方 加減法 代入法と文章題の計算方法 Hatsudy 総合学習サイト




画像の 3 のような分数と小数の混ざった連立方程式がわかりません 解 数学 教えて Goo



連立方程式の文章題 峠越え往復 チーム エン




無料 中2数学 基本問題 解答プリント 212 連立方程式5 文章問題1




中学2年の数学 動画 連立方程式 代入法編の問題 19ch




お勉強 連立方程式を楽に解く 数学は楽してなんぼ そらの暇つぶしch
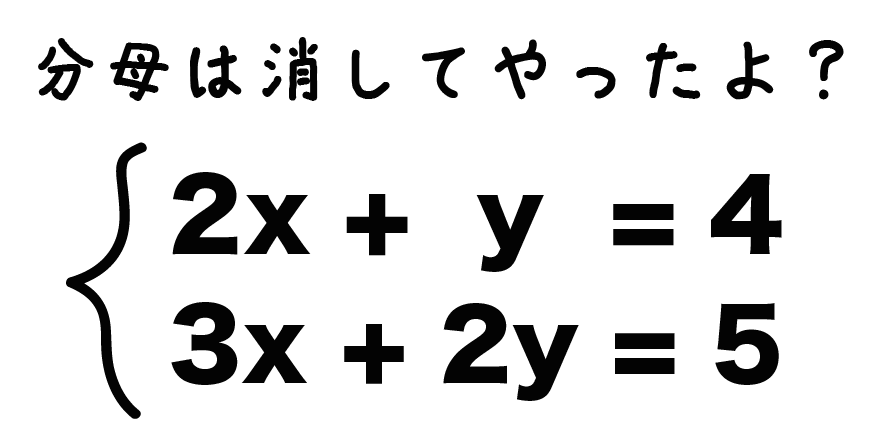



3分でわかる 分数をふくむ連立方程式の解き方 Qikeru 学びを楽しくわかりやすく




連立方程式の裏ワザ 加減法を使わずにサクッと解く方法 暇つぶしに動画で脳トレ



3分でわかる 分数をふくむ連立方程式の解き方 Qikeru 学びを楽しくわかりやすく




中2 P 53 連立方程式の計算特訓 Youtube




いろいろな形の連立方程式の計算問題 小数 分数 カッコ




分母の数が大きい場合の計算 連立方程式 中学生からの勉強質問 数学 進研ゼミ中学講座



1




中2数学 カッコ 分数を含む連立方程式 例題編 映像授業のtry It トライイット




連立方程式 分数を含む計算の解き方をイチから解説 Youtube
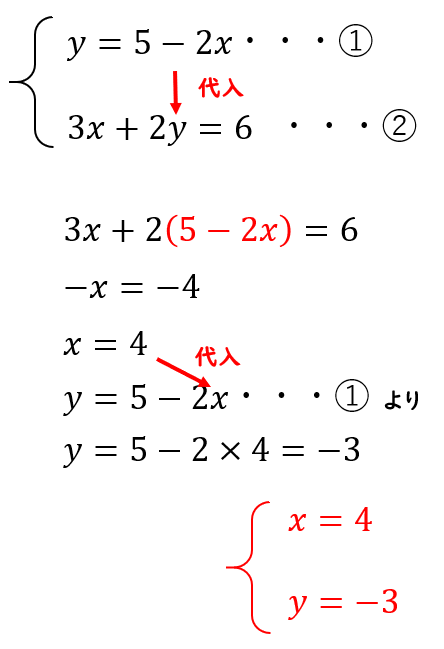



連立方程式の2つの解き方 代入法 加減法 数学fun
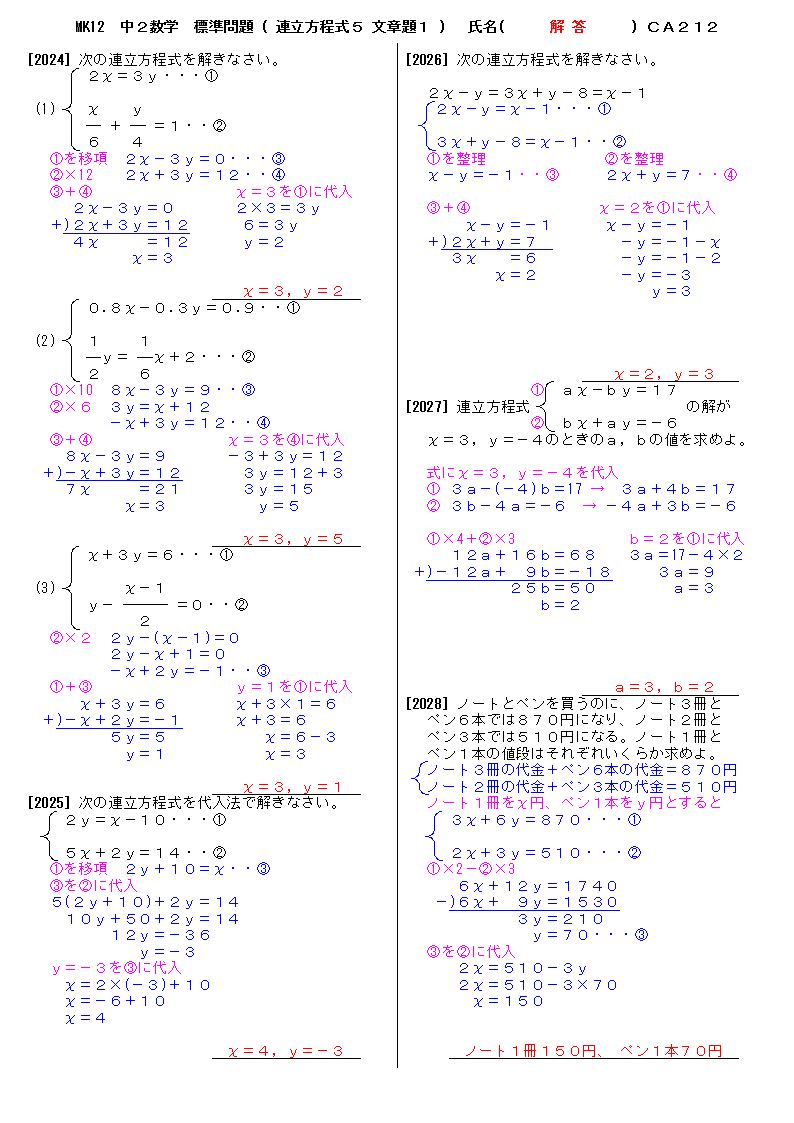



無料 中2数学 標準問題 解答プリント 212 連立方程式5 文章問題1
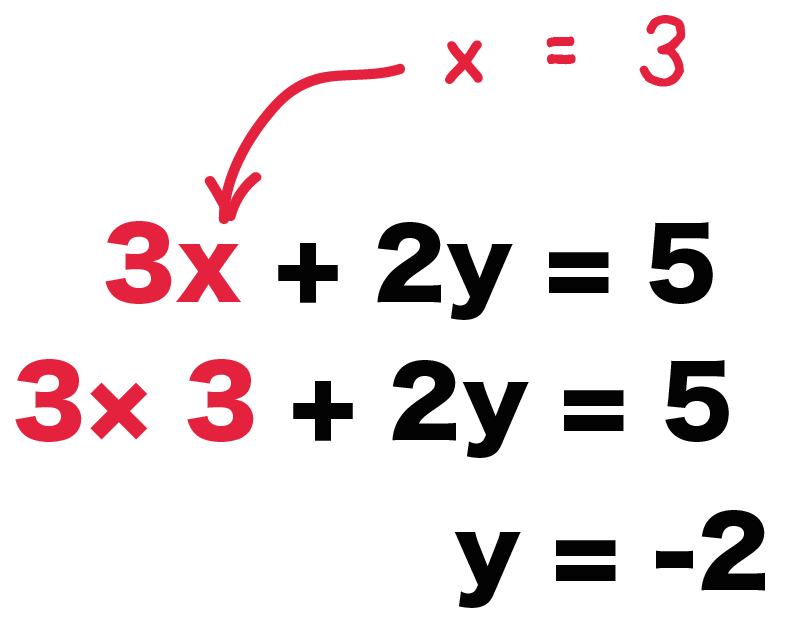



3分でわかる 分数をふくむ連立方程式の解き方 Qikeru 学びを楽しくわかりやすく




中学2年生 数学 連立方程式の活用 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中学数学2年 連立方程式 代入法 受験の月



連立方程式 分数




中学数学 連立方程式 の効果的な教え方 小数 分数問題
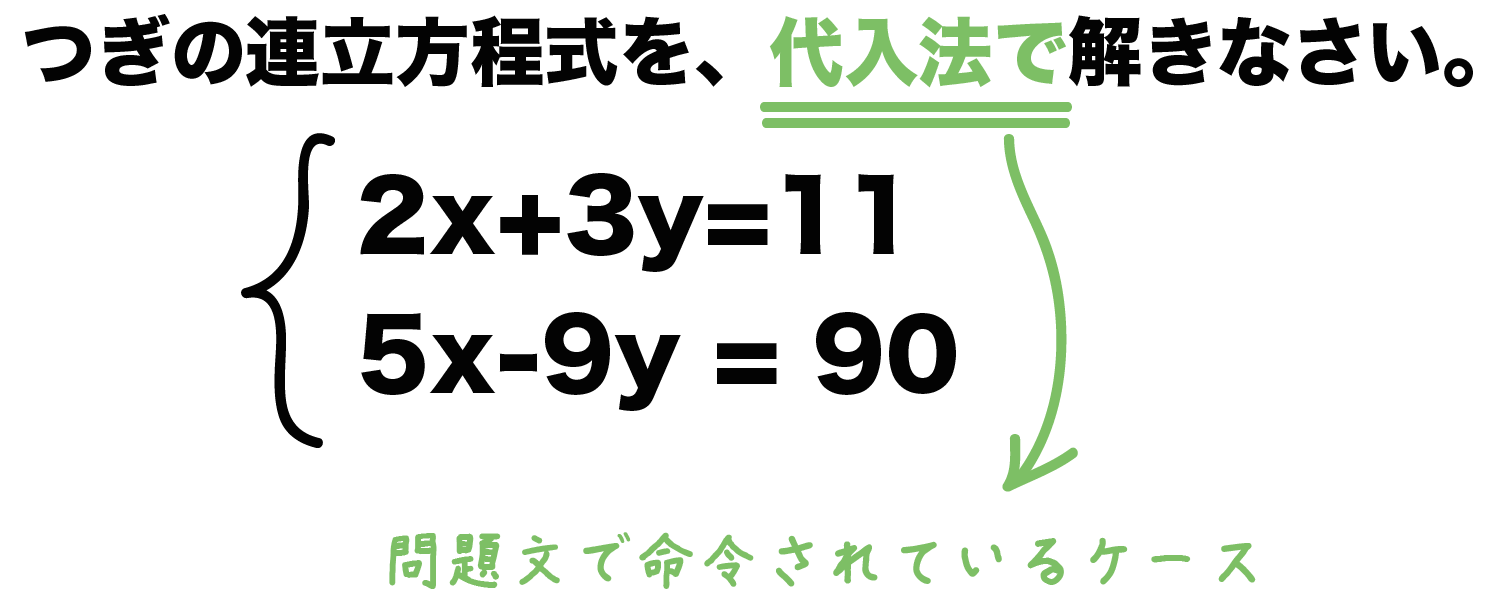



超簡単 連立方程式の解き方を見分ける2つのコツ Qikeru 学びを楽しくわかりやすく




連立方程式 分数と整数が混じった計算の解き方をイチから解説 中学数学 理科の学習まとめサイト



Studydoctor三元連立方程式 2 中2数学 Studydoctor




やさしい連立方程式を解こう 身勝手な主張




中2数学 カッコ 分数を含む連立方程式 練習編 映像授業のtry It トライイット



なるほど数学コラム 中学編 8 分母に文字がある連立方程式 を解こう Katekyo学院 教室で個別指導塾ならkatekyo学院 自宅でプロ家庭教師は福島県家庭教師協会 県内各地域で受講可能 福島 郡山 白河 会津 喜多方 いわき 相馬




無料 中2数学 発展問題 解答プリント 211 連立方程式4 複雑な式2




中2 連立方程式1 連立方程式とその解 中学数学の勉強に




中2数学 いろいろな連立方程式の解き方 学習プリント 練習問題 無料ダウンロード印刷




連立方程式の問題 高校の範囲でも登場する大切な分野だ 中学や高校の数学の計算問題



連立方程式の加減法 大人のやり直し算数の第一歩 計算方法の解説 無料



連立方程式の解が与えられている問題の解き方は 方程式の解き方まとめサイト




連立方程式 加減法 計算ドリル 問題集 数学fun




無料 中2数学 基本解説 問題プリント 211 連立方程式3 複雑な式



この連立方程式の解き方を教えてもらいたいです 教えてもらう立場で図々し Yahoo 知恵袋




いろいろな連立方程式 かっこを含む 分数 小数を含む A B C 教遊者




高校数学で学習する連立方程式の解き方まとめ 数スタ
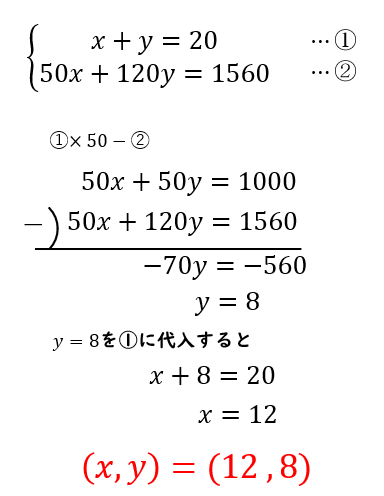



方程式練習問題 連立方程式の文章問題 個数と代金 方程式の解き方まとめサイト




中学数学 連立方程式 の効果的な教え方 導入と指導上の注意点




無料 中2数学 標準問題 解答プリント 213 連立方程式6 文章問題2




連立方程式の2つの解き方 代入法 加減法 数学fun



1




中2数学 連立方程式の利用 学習プリント 練習問題 無料ダウンロード印刷




中学2年生 数学 連立方程式の解き方 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中2数学 カッコ 分数を含む連立方程式 練習編 映像授業のtry It トライイット



連立方程式です 中2このプリントのこの問題がわかりません 答えはもら Yahoo 知恵袋
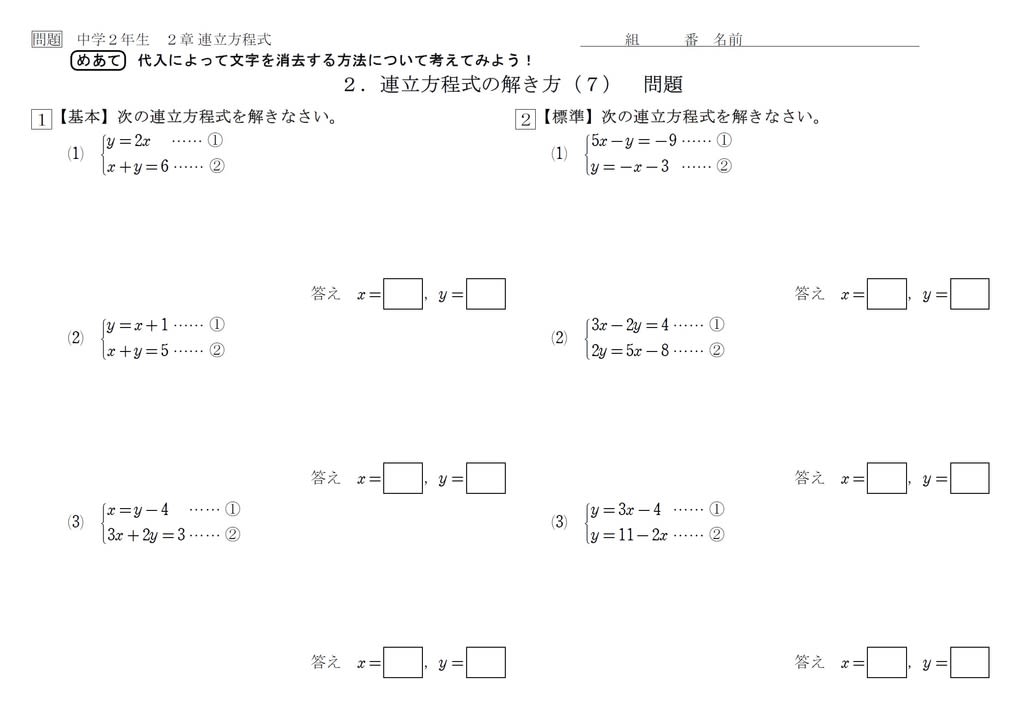



中2 連立方程式8 解き方7 中学数学の勉強に




連立方程式の解き方を説明しますー代入法を使った解き方ー おかわりドリル




中2数学 連立方程式の加減法2 係数をそろえる 練習編 映像授業のtry It トライイット




例題 演習問題付き 連立方程式の解き方と失敗しないコツをわかりやすく解説します




連立方程式 いろいろな計算 無料で使える中学学習プリント




3分でわかる 分数をふくむ連立方程式の解き方 Qikeru 学びを楽しくわかりやすく




中2数学 連立方程式の解き方 学習プリント 練習問題 無料ダウンロード印刷




3分でわかる 分数をふくむ連立方程式の解き方 Qikeru 学びを楽しくわかりやすく




中2数学 連立方程式 いろいろな連立方程式 4つのパターン たけのこ塾 勉強が苦手な中学生のやる気をのばす




連立方程式の解き方とは 代入法か加減法で計算しよう 分数の問題や文章題アリ 遊ぶ数学



中2数学連立方程式文字が分母にある問題です 解き方を教えてく Yahoo 知恵袋




連立方程式の加減法の解き方をマスターしたい方は見てください 中学や高校の数学の計算問題




中2数学 連立方程式の解き方と定期テスト予想問題 Pikuu




分数の連立方程式 Youtube




3分でわかる 小数をふくむ連立方程式の解き方 Qikeru 学びを楽しくわかりやすく




連立方程式を小学生に教える




小数の連立方程式の解き方 両辺を10倍や100倍しよう 中学や高校の数学の計算問題




高校数学で学習する連立方程式の解き方まとめ 数スタ




中学2年数学 分数と小数の連立方程式 勉強 Youtube スタディチューブ




中2数学 いろいろな連立方程式の解き方 学習プリント 練習問題 無料ダウンロード印刷



連立方程式とは 代入法と加減法 計算問題や文章題の解き方 受験辞典




世界一わかりやすい数学問題集中2 2章 連立方程式




中学2年生 数学 無料問題集 連立方程式を代入法で解く おかわりドリル




連立方程式の利用の問題の解き方 代金の問題 1 現役塾講師のわかりやすい中学数学の解き方
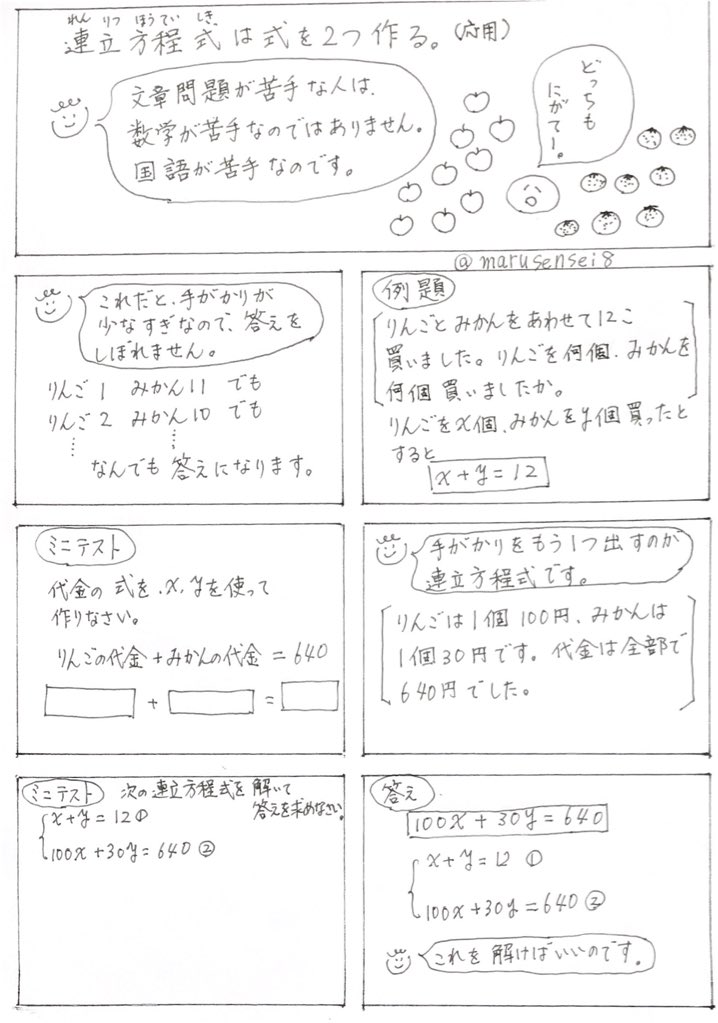



まる先生 連立方程式は式を2つ作る 文章問題の解き方 1 2 まる練 自宅学習 家庭学習 テスト対策 テスト勉強 マンガで勉強 高校入試 高校受験 まる練数学 中学数学 連立方程式 文章問題 T Co 0jbxo4ym5k Twitter
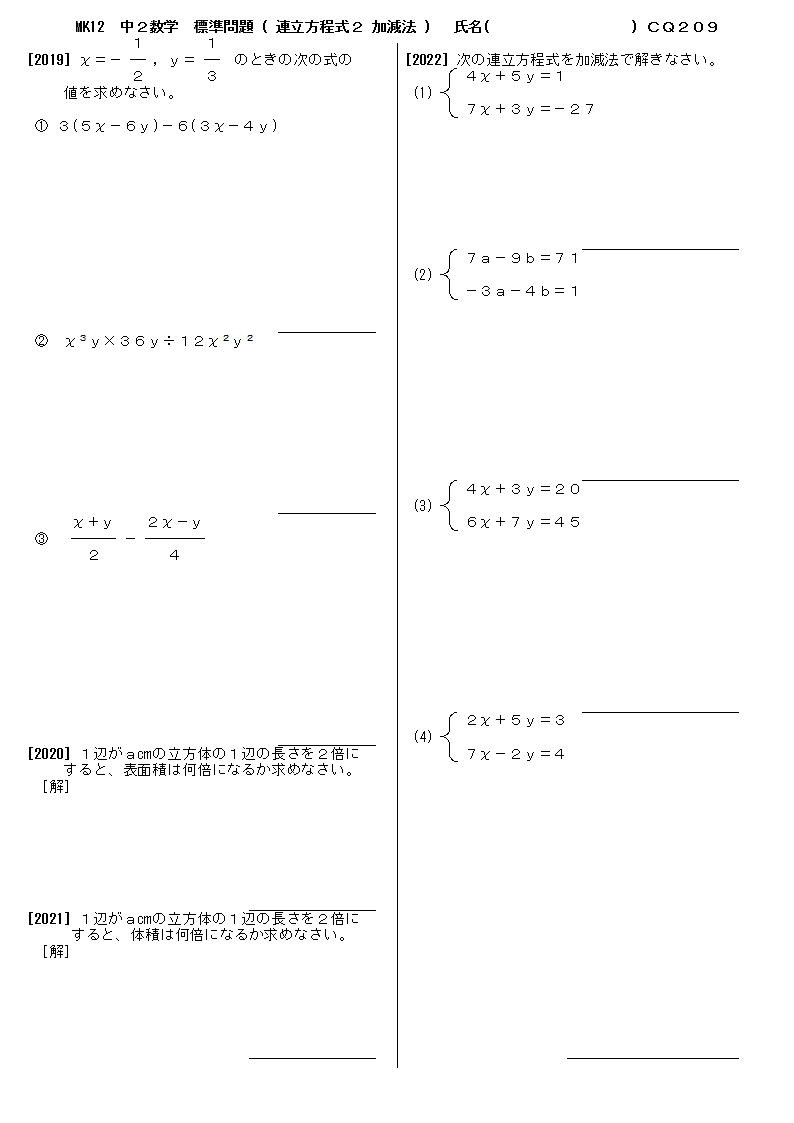



無料 中2数学 標準問題 問題プリント 9 連立方程式2 加減法




例題付き 連立方程式の解き方と失敗しないコツ




中学2年数学 分数と小数の連立方程式 Youtube



連立方程式の小数と分数の混ざった式について この問題が解 Yahoo 知恵袋



0 件のコメント:
コメントを投稿